[Fernando Isa Massa]: El problema P vs NP es uno de los problemas más importantes y conocidos en teoría de la computación y matemáticas. Es uno de los siete problemas del milenio identificados por el Clay Mathematics Institute y su resolución tiene una recompensa de un millón de dólares. A continuación, la historia y el contexto de este problema:

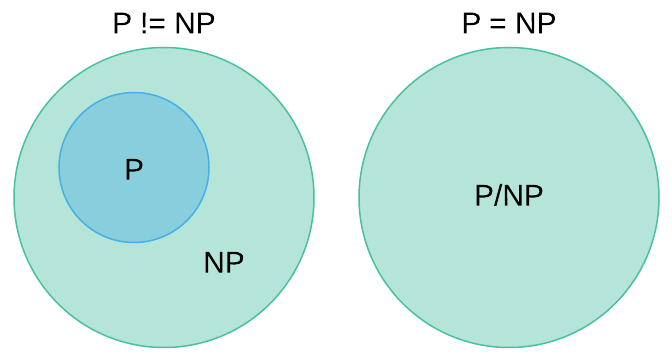
¿Qué es el problema P vs NP?: El problema P vs NP pregunta si las clases de complejidad P y NP son iguales o distintas. En términos simples:

–P: Es la clase de problemas de decisión que pueden ser resueltos por una máquina de Turing determinista en tiempo polinómico. Es decir, son problemas que pueden resolverse de manera eficiente (rápida) por una computadora.

–NP: Es la clase de problemas de decisión que pueden ser verificados por una máquina de Turing determinista en tiempo polinómico, pero no necesariamente resueltos en tiempo polinómico. Es decir, son problemas para los cuales, dada una solución propuesta, podemos verificar rápidamente si es correcta, pero no sabemos si existe un algoritmo eficiente para encontrar esa solución desde cero.

La pregunta central es: ¿P = NP? Es decir; ¿Todos los problemas que pueden ser verificados rápidamente también pueden ser resueltos rápidamente?

Historia del problema P vs NP:

1. Orígenes en la década de 1950 y 1960:

-El estudio de la complejidad computacional comenzó a tomar forma con el trabajo de Alan Turing y otros pioneros de la computación.

-En 1956, el matemático Kurt Gödel escribió una carta a John von Neumann en la que planteó una pregunta que es considerada precursora del problema P vs NP. Gödel preguntó si existía un algoritmo eficiente para resolver problemas de lógica proposicional (lo que hoy se conoce como el problema SAT).

2. Formalización en la década de 1970:

-El problema P vs NP fue formalizado de manera independiente por Stephen Cook y Leonid Levin en 1971.

–Stephen Cook introdujo el concepto de NP-completitud en su artículo seminal “The Complexity of Theorem Proving Procedures”(1971). Demostró que el problema SAT (el problema de satisfacibilidad booleana) es NP-completo, lo que significa que es uno de los problemas más difíciles en NP y que, si SAT tiene una solución eficiente, entonces todos los problemas en NP también la tendrían.

–Leonid Levin, en la Unión Soviética, llegó a conclusiones similares de manera independiente.

3. Desarrollo de la teoría de NP-completitud:

-Después del trabajo de Cook y Levin, Richard Karp demostró en 1972 que muchos otros problemas importantes son NP-completos, como el problema del clique, el problema del ciclo hamiltoniano y el problema del viajante (TSP). Esto consolidó la importancia del problema P vs NP.

4. El problema del milenio:

– En el año 2000, el Clay Mathematics Institute incluyó el problema P vs NP en su lista de los siete problemas del milenio, ofreciendo un premio de un millón de dólares por su resolución.

5.¿Por qué es importante?

El problema P vs NP tiene implicaciones profundas en matemáticas, ciencias de la computación, criptografía, inteligencia artificial y muchas otras áreas.

Si P=NP, significaría que problemas aparentemente difíciles, como el descifrado de claves criptográficas o la optimización de rutas, podrían resolverse de manera eficiente. Esto tendría un impacto enorme en la tecnología y la sociedad.

Por otro lado, si P≠NP, confirmaría que hay problemas que, aunque pueden ser verificados rápidamente, no pueden ser resueltos rápidamente. Esto justificaría el uso de métodos aproximados y heurísticos en la práctica.

6. Estado actual del problema:

Hasta la fecha, el problema P vs NP sigue sin resolverse. Aunque la mayoría de los expertos en computación creen que P≠NP, no se ha encontrado una prueba formal que lo demuestre. Se han realizado numerosos intentos para resolver el problema, incluyendo enfoques basados en teoría de la complejidad, geometría algebraica y física teórica, pero ninguno ha tenido éxito.

7. Conclusión:

El problema P vs NP es un desafío fundamental en la teoría de la computación que ha resistido más de 50 años de investigación intensa. Su resolución no sólo tendría un impacto teórico profundo, sino también práctico en campos como la criptografía, la optimización y la inteligencia artificial. Aunque aún no se ha resuelto, sigue siendo una de las preguntas más fascinantes y motivadoras en la ciencia moderna.

En la teoría de la computación, los problemas se clasifican en diferentes clases de complejidad según cuántos recursos (como tiempo y espacio) se necesitan para resolverlos. Dos de las clases de problemas más importantes son P y NP, que representan conjuntos de problemas con características específicas. A continuación, se explica qué son los problemas P y los problemas NP, y cómo se diferencian.

Problemas P: Los problemas P son aquellos que pueden ser resueltos por una máquina de Turing determinista en tiempo polinómico. En términos más simples:

Definición: Un problema está en la clase P si existe un algoritmo que puede resolverlo en un tiempo que crece de manera polinómica con respecto al tamaño de la entrada. Es decir, si el tamaño de la entrada es (n\), el tiempo de ejecución del algoritmo es (O(n^k)), donde (k) es una constante.

Ejemplos:

1. Ordenar una lista de números: Algoritmos como QuickSort o MergeSort pueden ordenar una lista en tiempo (O(n\log n)).

2. Buscar un elemento en un arreglo ordenado: La búsqueda binaria resuelve este problema en tiempo (O(\log n)).

3. Verificar si un número es primo: El algoritmo AKS prueba la primalidad en tiempo polinómico.

-Importancia: Los problemas en P se consideran “fáciles” o “tratables” porque pueden resolverse de manera eficiente, incluso para entradas grandes.

Problemas NP: Los problemas NP son aquellos que pueden ser verificados por una máquina de Turing determinista en tiempo polinómico. Es decir, dada una solución propuesta, podemos verificar rápidamente si es correcta, pero no necesariamente sabemos cómo encontrar esa solución de manera eficiente.

Definición: Un problema está en la clase NP si, dada una solución candidata, existe un algoritmo que puede verificar si esa solución es correcta en tiempo polinómico. Además, NP incluye todos los problemas en P, ya que, si un problema puede resolverse en tiempo polinómico, también puede verificarse en tiempo polinómico.

Ejemplos:

1. Problema del viajante (TSP): Dado un conjunto de ciudades y distancias; ¿Existe una ruta que visite todas las ciudades exactamente una vez y tenga una longitud total menor o igual a un valor dado? Verificar una ruta propuesta es fácil, pero encontrar la ruta óptima es difícil.

2. Problema de la mochila: Dado un conjunto de objetos con pesos y valores; ¿Existe una selección de objetos que no exceda un peso máximo y tenga un valor total mayor o igual a un valor dado? Verificar una selección es fácil, pero encontrar la selección óptima es difícil.

Importancia: Los problemas en NP son fundamentales en la teoría de la computación porque muchos problemas prácticos, como la planificación, la optimización y la criptografía, caen en esta categoría.

Ante lo expuesto se plantean nuevos paradigmas, nuevos modelos en lógica, álgebra y geometría. La geometría que introduce una interpretación de la geometría Euclidiana generando una geometría no Euclidiana. Desde la teoría de la relatividad se usan geometrías no Euclidianas para conceptualizar fenómenos complejos de muy difícil interpretación y desarrollo matemático. La nueva geometría no Euclidiana se basa en uno de los postulados de Euclides, cuya contradicción lleva a conceptos llenos de interpretaciones matemáticas y a un alto nivel de abstracción de los modelos. Es un desafío encontrar la realidad y la relación entre la geometría no Euclidiana y el problema NP versus P, por lo tanto, y dado la compleja forma matemática de tales aseveraciones; cabría la posibilidad de encontrar un nexo que relaciona lo exponencial con lo no exponencial del problema.

No se pretende afirmar que el problema está resuelto, solo una astuta y compleja deducción, nos lleva a nuevos paradigmas, y con ellos a dudar, como una forma acertada de construcción del método científico. No se puede confirmar o rechazar el problema con las matemáticas actuales, esto quedó en evidencia después de muchos intentos de matemáticos brillantes. Es un problema que nos sugiere, dado los fallidos intentos, a buscar nuevos horizontes científicos y esa tarea es complementada, a su vez, con el criterio y sentido común que la ciencia requiere.

También, se introducen conceptos relacionados a complejas abstracciones en álgebras renovadas, razón por la cual, y como es de interés de los matemáticos unir disciplinas distintas, es un reflejo no sólo del conocimiento sino de lo circunstancial y relacionados que son los métodos de las matemáticas. Esta álgebra refleja la comunicación entre dos áreas de las matemáticas deterministas: la geometría y el álgebra; por eso enriquece el saber, introducir elementos de otras áreas como son las probabilidades y el caos. Sería un ejemplo de cómo las matemáticas no funcionan solas, sino que se complementan en la búsqueda de soluciones viables y que no sólo están enfocadas al ambiente científico. Los que están fuera de las matemáticas encontrarán en el diseño conceptual del problema, una respuesta a sus propias decisiones e hipótesis, lo que nos lleva a pensar en la universalidad de la ciencia y de las matemáticas más específicamente.

Todavía el enfoque está sesgado por la intuición y quedará al mundo científico, evaluar el método y los resultados. La interpretación no es sencilla. Nos lleva a nuevas abstracciones y la caída de viejos paradigmas; para incorporar nuevas e hipotéticas soluciones. Es el comienzo, la verdad es hija del tiempo y esta verdad se desprende de la intuición y la consabida inteligencia y espíritu humano de vencer las adversidades. Este mismo espíritu que nos hace hacedores del progreso y desarrollo de las especies, como así también sus verdugos.

Fernando Isa Massa es Analista Universitario de Sistemas [Universidad Tecnológica Nacional], disertante en diversos foros científicos, ha publicado en numerosas revistas científicas de Ciencias Exactas]